Algorithmic trading systems are sets of rules that automate the investment process. By trading systematically, algorithmic traders enjoy several advantages over traditional investors. It is often easier to predict the future performance of a systematic strategy than a heuristic strategy because the rules underlying a systematic strategy are well-defined, static in time and (ideally) sheltered from the biases of human intervention. Algorithmic traders can also react quickly to new information about the market, so they can often outperform human traders when performance is latency dependent.
However, algorithmic traders face many challenges: markets are complex; predicting which investment strategies will perform well and distilling these strategies into a set of rules that can be executed by a trading system are difficult tasks. Markets are also constantly evolving, so while the rules underlying a systematic strategy should be static, their predictions must be able to evolve with the market.
Machine learning (ML) provides tools for the systematic investor to overcome these challenges. Often meant to mimic human learning, these algorithms find patterns in training data that allow them to draw conclusions about new, unseen data. Machine learning algorithms can learn complex patterns and adapt as the data evolve, making them good candidates for the systematic investor’s toolbox. In this blog post, we discuss how members of Maven’s Systematic Alpha team use machine learning and some of the challenges they face.
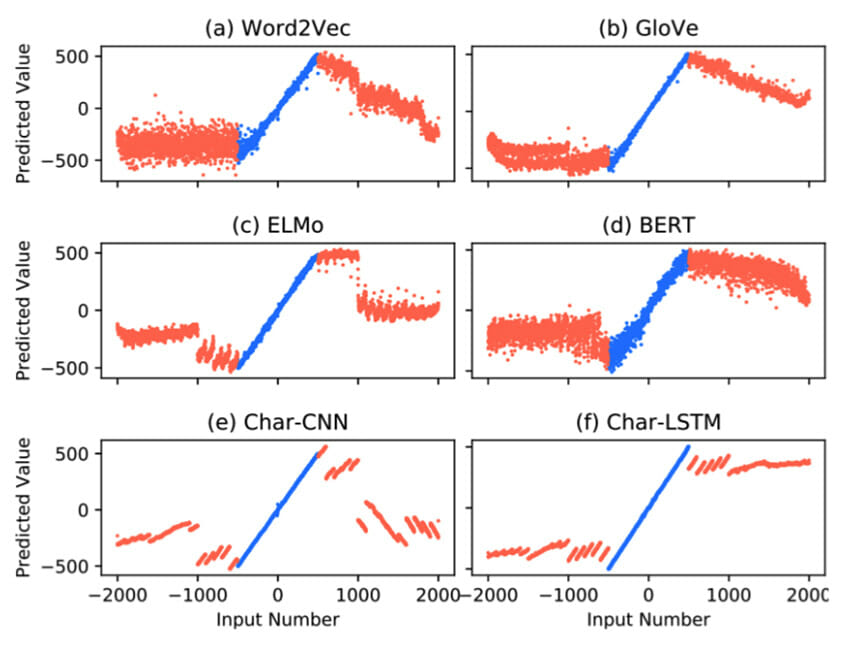
Figure 1 from Wallace et al. . The researchers use the outputs of different word embedding models to map a numeral to a number (e.g. “71” to 71.0). The models are trained using numerals between -500 and 500 (the blue region), and tested on the interval -2000 to 2000. BERT is one of the worst performers on this task, showing that it struggles to capture numerical information in its embeddings.
An example from natural language processing (NLP)
Language is an obvious influencer of market dynamics. News, executive interviews, and customer reviews are all sources of language that could affect stock prices. For a systematic trader to use this information, the trading system must be able to extract information from natural language. NLP is a decades-long research effort to develop algorithms that extract this information. At Maven, we work to optimise state-of-the-art techniques from NLP for algorithmic trading.
BERT-based models, first introduced by Devlin et al. , are deep neural networks that have demonstrated state-of-the-art performance on many NLP tasks, for example, classifying the sentiment of a sentence. Despite their strong performance, more research is required to optimise them for algorithmic trading systems. For example, BERT-based models have been shown to be worse than their predecessors on tasks involving numerical reasoning. Figure 1 shows that BERT-based models have trouble decoding a numeral, such as the text “71”, to its actual numerical value, so it is not able to capture ordinal relationships like “70 is less than 71” when it is extracting information from text. This is a significant problem in financial applications, where relevant text often involves numbers and numerical comparisons. Creating BERT-like models with better numerical reasoning skills is an active area of research that significantly affects the performance of algorithmic trading systems.
Overfitting and noise
A general misconception about ML models is that they are difficult to understand, “black boxes” that are prone to overfitting. Indulging this view, it could be dangerous to use complex ML models in the investment process because it could be difficult to tell if they have overfit or if they have extracted genuinely predictive patterns. Combatting overfitting is particularly important in finance, where signal-to-noise ratios are so low that it can be difficult to distinguish between statistically significant performance and lucky guesses. There are many methods to reduce overfitting; here we discuss two: decreasing model complexity through regularisation, and increasing model complexity into the “interpolative regime”.
Regularisation methods penalise a model’s complexity so that during training, a model learns parameters that minimise error on the training data as well as the parameters’ complexity. The “complexity” of a model can be defined in various ways, typical examples include the magnitude of the model’s parameters or the number of non-zero parameters. Training a typical ML model with regularisation involves finding model parameters that solve the following optimisation problem:
minimise (error on training data + regularisation term)
The more regularisation, the less is the potential for overfitting. A good choice of regulariser not only reduces model complexity but also encourages structure in the model that represents prior knowledge about the solution. Constructing regularisation methods that incorporate prior knowledge about market behaviour can significantly improve the performance of a trading system.
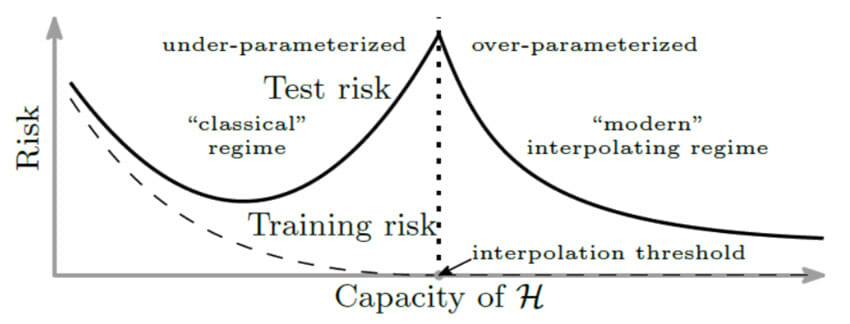
Figure 2 from Belkin . Classical understanding of ML suggests that as models become more complex, they fit training data more precisely, but their performance on unseen data starts to suffer. Recent research is extending this model into the “interpolating” regime, where models achieve zero error on the training data, but counterintuitively, their performance continues to improve on unseen data.
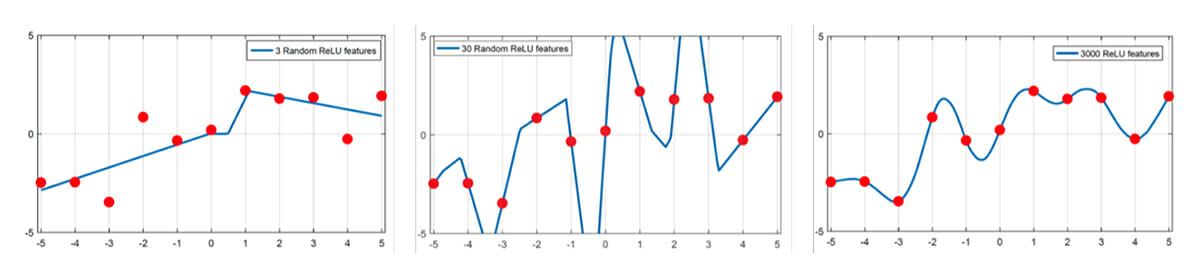
Figure 3 from Belkin . A demonstration of the generalisation curves in Figure 2 using a shallow network with ReLU activations for regression. With 30 nodes, the network is able to perfectly interpolate the data, but the fit is unstable and the model is unlikely to generalise. With 3000 nodes, the model is able to find a smooth interpolator of the data, achieving perfect training performance and producing a model that is likely to generalise.
Finding the right balance between fitting the data and generalising well on unseen data has been at the centre of traditional ML. However, recent research suggests that over-parameterization is not synonymous with overfitting, and increasing model complexity can counter-intuitively improve generalisation. Experimenters have long observed that deep neural networks can achieve perfect accuracy on training data and still perform well on unseen data. Such models, operating in the “interpolative regime” because they perfectly interpolate the training data, avoid overfitting because their hyper-complexity allows them to find “optimal” interpolators, such as the “smoothest” curve that perfectly covers the training data. Figure 2 shows the relationship between model generalisation and complexity in the classical and interpolating regimes, and Figure 3 exemplifies this using a shallow ReLU network for simple regression.
While this burgeoning theory of over-parameterised models is able to explain the superiority of deep learning models in many applications, research is ongoing to determine if similar conclusions hold in financial applications. With the extremely low signal-to-noise ratios characteristic to problems in finance, interpolative models are not always appropriate because they overemphasise the effects of outliers in the data. Explaining when hyper-parameterised models are effective in noisy datasets is a principal research question in systematic trading.
ML Research at Maven
When developing systematic trading strategies at Maven, keeping up with the latest research is only half the work. State-of-the-art models provide a starting point, but they require adaptation and further research before they are applicable to our problems. A constantly evolving market requires continuous research just to keep pace, but the result: having a robust, reliable, best-in-class trading system, is worth the effort.
E. Wallace, Y. Wang, S. Li, S. Singh, and M. Gardner. “Do NLP Models Know Numbers?”. In EMNLP-IJCNLP. (2019).
J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova. “BERT: pre-training of deep bidirectional transformers for language understanding”. In NAACL. (2019).
M. Belkin. “Fit without fear: remarkable mathematical phenomena of deep learning through the prism of interpolation”. arXiv preprint arXiv:2105.14368. (2021).